
算法6
计算三叉搜索树的高度
定义构造三叉搜索树规则如下: 每个节点都存有一个数,当插入一个新的数时,从根节点向下寻找,直到找到一个合适的空节点插入查找的规则是:
1.如果数小于节点的数减去500,则将数插入节点的左子树
2.如果数大于节点的数加上500,则将数插入节点的右子树
3.否则,将数插入节点的中子树
给你一系列数,请按以上规则,按顺序将数插入树中,构建出一棵三叉搜索树,最后输出树的高度。
输入描述:
- 第一行为一个数N,表示有N个数,
1<=N<=10000 - 第二行为N个空格分隔的整数,每个数的范围为
[1,10000]
输出描述:输出树的高度(根节点的高度为1)
输入
5
5000 2000 5000 8000 1800
输出
3
说明
最终构造出的树如下,高度为3class TreeNode {
constructor(val) {
this.val = val;
this.left = null;
this.mid = null;
this.right = null;
}
}
class Tree {
insert (root, val) {
if (root === null) {
return new TreeNode(val);
}
if (val < root.val - 500) {
root.left = this.insert(root.left, val)
} else if (val > root.val + 500) {
root.right = this.insert(root.right, val)
} else {
root.mid = this.insert(root.mid, val)
}
return root; // 返回根节点
}
getHeight (root) {
if (root === null) {
return 0;
}
let leftHeight = this.getHeight(root.left);
let midHeight = this.getHeight(root.mid);
let rightHeight = this.getHeight(root.right);
return Math.max(leftHeight, midHeight, rightHeight) + 1;
}
}
let tree = new Tree();
let root = null;
const readline = require('readline')
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
})
rl.on('line', (line) => {
const N = parseInt(line);
rl.on('line', (line2) => {
const numbers = line2.split(' ').map(Number);
for (let number of numbers) {
root = tree.insert(root, number)
}
const height = tree.getHeight(root);
console.log(height);
})
})石头剪刀布游戏
石头剪刀布游戏有 3 种出拳形状:石头、剪刀、布。分别用字母 A , B , C 表示。
游戏规则:
出拳形状之间的胜负规则如下: A > B;B > C;C > A;">"左边一个字母,表示相对优势形状。右边一个字母,表示相对劣势形状。 当本场次中有且仅有一种出拳形状优于其它出拳形状,则该形状的玩家是胜利者。否则认为是平局。 当发生平局,没有赢家。有多个胜利者时,同为赢家。
例如 1: 三个玩家出拳分别是A, B, C ,由于出现三方优势循环(即没有任何一方优于其它出拳者),判断为平局。
例如 2: 两个玩家,出拳分别是 A, B ,出拳 A 的获胜。
例如 3: 三个玩家,出拳全部是 A ,判为平局。
输入描述:
在一场游戏中,每个玩家的信息为一行。玩家数量不超过 1000 。每个玩家信息有 2 个字段,用空格隔开:
玩家 ID:一个仅由英文字母和数字组成的字符串 出拳形状:以英文大写字母表示, A 、B 、C 形状。 例:
abc1 A
xyz B输出描述:
输出为赢家的玩家 ID 列表(一个或多个),每个 ID 一行,按字符串升序排列。如果没有赢家,输出为"NULL"字符串。例如:
abc1abc1 A
xyz A
输出 NULLconst readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
})
let shapeMap = new Map();
rl.on('line', (line) => {
const [palyerId, shape] = line.split(' ')
if (shapeMap.has(shape)) {
shapeMap.get(shape).push(playerId)
} else {
shapeMap.set(shape, [playerId])
}
}).on('close', () => {
if (shapeMap.size !== 2) {
console.log('NULL')
process.exit(0)
}
let winners;
if (shapeMap.has('A') && shapeMap.has('B')) {
winners = shapeMap.get('A');
} else if (shapeMap.has('B') && shapeMap.has('C')) {
winners = shapeMap.get('B');
} else if (shapeMap.has('C') && shapeMap.has('A')) {
winners = shapeMap.get('C');
} else {
console.log('NULL')
process.exit(0)
}
winners.sort()
for (let i = 0; i < winners.length; i++) {
console.log(winners[i])
}
})多段数据压缩
下图中,每个方块代表一个像素,每个像素用其行号和列号表示。为简化处理,多段线的走向只能是水平、竖直、斜向45度。
上图中的多段线可以用下面的坐标串表示:(2, 8), (3, 7), (3, 6), (3, 5), (4, 4), (5, 3), (6, 2), (7, 3), (8, 4), (7, 5)。
但可以发现,这种表示不是最简的,其实只需要存储6个蓝色的关键点即可,它们是线段的起点、拐点、终点,而剩下4个点是冗余的。
即可以简化为:(2,8)、(3,7)、(3,5)、(6,2)、(8,4)、(7,5)
现在,请根据输入的包含有冗余数据的多段线坐标列表,输出其最简化的结果。
输入描述:
2 8 3 7 3 6 3 5 4 4 5 3 6 2 7 3 8 4 7 5
- 1、所有数字以空格分隔,每两个数字一组,第一个数字是行号,第二个数字是列号;
- 2、行号和列号范围为
[0,64),用例输入保证不会越界,考生不必检查; - 3、输入数据至少包含两个坐标点。
输出描述:
2 8 3 7 3 5 6 2 8 4 7 5
- 压缩后的最简化坐标列表,和输入数据的格式相同。
备注: 输出的坐标相对顺序不能变化。
function isTrunPoint(prev, curr, next) {
const dx1 = curr[0] - prev[0]
const dy1 = curr[1] - prev[1]
const dx2 = next[0] - curr[0]
const dy2 = next[1] - curr[1]
return dx1 * dy2 !== dy1 * dx2;
}
function simplifyPath(points) {
if (points.length < 2) return points;
const result = [points[0]]
for (let i = 1; i < points.length - 1; i++) {
if (isTrunPoint(points[i - 1], points[i], points[i + 1])) {
result.push(point[i])
}
}
}
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
})
const points = []
rl.on('line', (line) => {
const nums = line.split(' ').map(Number);
for (let i = 0; i < nums.length; i += 2) {
points.push([nums[i], nums[i + 1]])
}
el.close()
}).on('close', () => {
const simplifiedPoints = simplifyPath(points);
const output = simplifiedPoints.map(point => {
return point.join(' ')
}).join(' ')
console.log(output);
process.exit(0);
})求字符串中所有整数的最小和
输入字符串s,输出s中包含所有整数的最小和
说明
- 字符串s,只包含
a-z A-Z +-; - 合法的整数包括
- 1)正整数 一个或者多个0-9组成,如 0 2 3 002 102
- 2)负整数 负号 - 开头,数字部分由一个或者多个0-9组成,如 -0 -012 -23 -00023
输入描述:包含数字的字符串
输出描述:所有整数的最小和
输入:
bb1234aa
输出:
10
bb12-34aa
输出 -31
说明 1 + 2 - 34 = 31;function getMinSum (str) {
let numArr = str.split(/[^\d-]+/);
let res = 0;
function getNumSum(num) {
let sum = 0;
for (let c of num) {
sum += parseInt(c);
}
return sum;
}
for (let i = 0; i < numArr.length; i++) {
if (numArr[i]) {
if (numArr[i].indexOf('-') === -1) {
res += getNumSum(numArr[i]);
} else {
let isNeg = numArr[i].startsWith('-');
let subStrs = numArr[i].split('-');
for (let i = 0; i < subStrs.length; i++) {
if (subStrs[i]) {
let ele = parseInt(subStrs[i])
if (i === 0) {
res += isNeg ? (0 - ele) : getNumSum(subStrs[i])
} else {
res -= ele;
}
}
}
}
}
}
console.log(res);
}求幸存数之和
给一个正整数列nums,一个跳数jump,及幸存数量left。运算过程为:
- 从索引为0的位置开始向后跳,中间跳过 J 个数字,命中索引为 J+1的数字,该数被敲出,并从该点起跳,以此类推,直到幸存left个数为止。然后返回幸存数之和。
约束:
0是第一个起跳点。
起跳点和命中点之间间隔jump 个数字,已被敲出的数字不计入在内。
跳到末尾时无缝从头开始(循环查找),并可以多次循环。
若起始时 left > len(nums) 则无需跳数处理过程。
/**
*
* @param nums 正整数数列,长度范围 [1,10000]
* @param jump 跳数,范围 [1,10000]
* @param left 幸存数量,范围 [1,10000]
* @return 幸存数之和
*/
int sumOfLeft(int[] nums,int jump,int left)输入:
[1,2,3,4,5,6,7,8,9],4,3
输出:
13
说明:
从1(索引为0)开始起跳,中间跳过4个数字因此依次删除 6,2,8,5,4,7。 剩余 1,3,9,返回和为13const readline = require('readline')
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
})
let nums = []
let jump = 0;
let left = 0;
rl.on('line', (line) => {
if (!this.nums.length) {
this.nums = line.split(',').map(Number)
} else if (!jump) {
jump = parseInt(line);
} else if (!left) {
left = parseInt(line);
console.log(sumOfLeft(nums, jump, left))
rl.close()
}
})
function sumOfLeft(nums, jump, left) {
if (left >= nums.length) {
return nums.reduce((acc, cur) => {
return acc + cur
}, 0)
}
let index = 0;
let list = nums.slice();
while (list.length > left) {
index = (index + jump + 1) % list.length;
list.splice(index, 1)
index = index - 1;
}
return list.reduce((acc, cur) => {
return acc + cur;
}, 0)
}悄悄话
给定一个二叉树,每个节点上站一个人,节点数字表示父节点到该节点传递悄悄话需要花费的时间。
初始时,根节点所在位置的人有一个悄悄话想要传递给其他人,求二叉树所有节点上的人都接收到悄悄话花费的时间。
输入描述:
0 9 20 -1 -1 15 7 -1 -1 -1 -1 3 2 (-1 表示空节点)
输出描述:返回所有节点都接收到悄悄话花费的时间
const readline = require('readline')
const rl = readline.createInterface({
input: process.stdin,
output: process.steout,
})
rl.on('line', (line) => {
const allNums = line.split(' ').map(Number)
let maxTime = 0;
const nodeQueue = []
nodeQueue.push(0);
while (nodeQueue.length) {
const parentNodeIndex = nodeQueue.shift();
const leftIndex = 2 * parentNodeIndex + 1;
const rightIndex = 2 * parentNodeIndex + 2;
if (leftIndex < allNums.length && allNums[leftIndex] !== -1) {
allNums[leftIndex] += allNums[parentNodeIndex]
nodeQueue.push(leftIndex)
maxTime = Math.max(maxTime, allNums[leftIndex])
}
if (rightIndex < allNums.length && allNums[rightIndex] !== -1) {
allNums[rightIndex] += allNums[parentNodeIndex]
nodeQueue.push(rightIndex)
maxTime = Math.max(maxTime, allNums[rightIndex])
}
}
console.log(maxTime);
rl.close();
})密码解密
给定一段“密文”字符串 s,其中字符都是经过“密码本”映射的,现需要将“密文”解密并输出。
映射的规则('a' ~ 'i')分别用('1' ~ '9')表示;('j' ~ 'z')分别用("10*" ~ "26*")表示。
约束:映射始终唯一。
输入描述:“密文”字符串
输出描述:明文字符串
备注:翻译后的文本长度在100以内
20*19*20*
输出tstconst readline = require('readline')
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
})
rl.on('line', (line) => {
let s = line;
const replaceEles = Array.from({
length: 26
}, (_, i) => {
return [i + 1, String.fromCharCode(97 + i)]
})
replaceEles.reverse().forEach(([key, val]) => {
s = s.replaceAll(key >= 10 ? `${key}*` : key.toString(), val);
})
console.log(s)
})生成哈夫曼树
给定长度为 n 的无序的数字数组,每个数字代表二叉树的叶子节点的权值,数字数组的值均大于等于 1 。
请完成一个函数,根据输入的数字数组,生成哈夫曼树,并将哈夫曼树按照中序遍历输出。
为了保证输出的二叉树中序遍历结果统一,增加以下限制:
- 在树节点中,左节点权值小于等于右节点权值,根节点权值为左右节点权值之和。
- 当左右节点权值相同时,左子树高度高度小于等于右子树。
注意: 所有用例保证有效,并能生成哈夫曼树提醒:哈夫曼树又称最优二叉树,是一种带权路径长度最短的一叉树。
所谓树的带权路径长度,就是树中所有的叶结点的权值乘上其到根结点的路径长度(若根结点为 0 层,叶结点到根结点的路径长度为叶结点的层数)
输入描述:
例如:由叶子节点 5 15 40 30 10 生成的最优二叉树如下图所示,该树的最短带权路径长度为 40∗1+30∗2+15∗3+5∗4+10∗4=205。
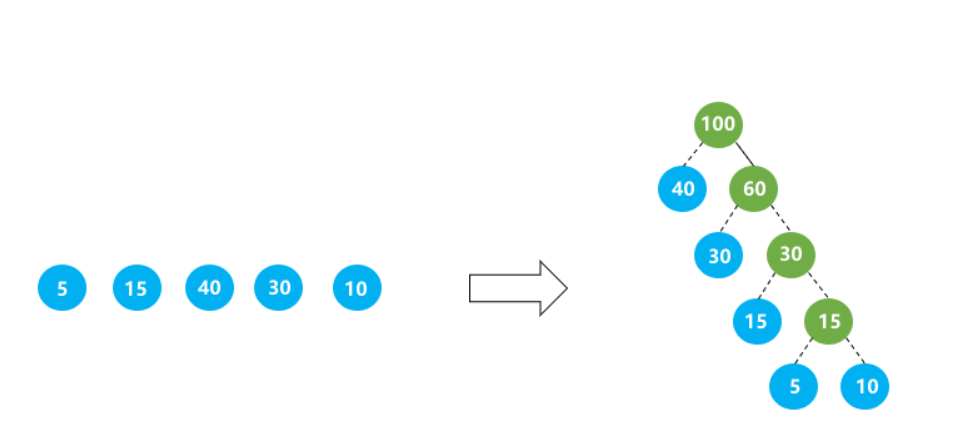
输出描述:输出一个哈夫曼的中序遍历数组,数值间以空格分隔
输入:
5
5 15 40 30 10
输出:
40 100 30 60 15 30 5 15 10
说明:
根据输入,生成哈夫曼树,按照中序遍历返回。所有节点中,左节点权值小于等于右节点权值之和。当左右节点权值相同时左子树高度小于右子树。结果如上图class Node {
constructor (value) {
this.value = value;
this.left = null;
this.right = null;
}
}
class MinPriorityQueue {
constructor () {
this.elements = []
}
enqueue(element) {
this.elements.push(element);
this.elements.sort((a, b) => a.value - b.value);
}
dequeue() {
return this.elements.shift(); // 移除并返回数组第一个元素
}
isEmpty() {
return this.elements.length === 0;
}
}
function buildHuffmanTree (values) {
const pq = new MinPriorityQueue();
values.forEach(value => {
pq.enqueue(new Node(value))
})
while (pq.elements.length > 1) {
let left = pq.dequeue();
let right = pq.dequeue();
const parent = new Node(left.value + right.value);
parent.left = left;
parent.right = right;
pq.enqueue(parent);
}
return pq.dequeue();
}
function inorderTraversal(root) {
if (root) {
inorderTraversal(root.left);
console.log(root.value)
inorderTraversal(root.right);
}
}
const readline = require('readline')
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout
})
rl.on('line', (n) => {
rl.on('line', (line) > {
const values = line.split(' ').map(Number)
const root = buildHuffmanTree(values);
const result = ''
console.log(reslut);
rl.close();
})
})核酸检测
为了达到新冠疫情精准防控的需要,为了避免全员核酸检测带来的浪费,需要精准圈定可能被感染的人群。
现在根据传染病流调以及大数据分析,得到了每个人之间在时间、空间上是否存在轨迹的交叉。
现在给定一组确诊人员编号 (X1,X2,X3,…Xn)在所有人当中,找出哪些人需要进行核酸检测,输出需要进行核酸检测的数。
(注意:确诊病例自身不需要再做核酸检测)需要进行核酸检测的人,是病毒传播链条上的所有人员,即有可能通过确诊病例所能传播到的所有人。
例如:A是确诊病例,A和B有接触、B和C有接触 C和D有接触,D和E有接触。那么B、C、D、E都是需要进行核酸检测的人
输入描述:
- 第一行为总人数N
- 第二行为确证病例人员编号
(确证病例人员数量<N),用逗号隔开 - 接下来N行,每一行有N个数字,用逗号隔开,其中第i行的第j个数字表名编号i是否与编号j接触过。0表示没有接触,1表示有接触
备注:
- 人员编号从0开始
0 < N < 100 0<N<1000<N<100
输出描述:输出需要做核酸检测的人数
5
1,2
1,1,0,1,0
1,1,0,0,0
0,0,1,0,1
1,0,0,1,0
0,0,1,0,1
输出 3// num 5;
// confirmedCases 1,2
// inputs ['1,1,0,1,0', '1,1,0,0,0']
function getHesuanNum (num, confirmedCases, inputs) {
let confirm = confirmedCases.split(',').map(Number);
let visited = new Array(num).fill(false);
let contacts = Array.from({ length: num }, () => {
return Array(num).fill(false);
})
inputs.forEach((value, index) => {
let split = value.split(',')
contacts[index] = split.map(value => value == 1);
})
console.log('contacts', contacts);
function dfs (contacts, visited, start) {
visited[start] = true;
for (let i = 0; i < contacts.length; i++) {
if (contacts[start][i] && !visited[i]) {
dfs(contacts, visited, i);
}
}
}
confirm.forEach((value) => {
dfs(contacts, visited, value);
})
console.log('visited', visited);
let count = 0;
visited.forEach((hasVisited, index) => {
if (hasVisited && !confirm.includes(index)) {
count++;
}
})
console.log(count);
}贪吃的猴子
一只贪吃的猴子,来到一个果园,发现许多串香蕉排成一行,每串香蕉上有若干根香蕉。每串香蕉的根数由数组numbers给出。猴子获取香蕉,每次都只能从行的开头或者末尾获取,并且只能获取N次,求猴子最多能获取多少根香蕉。
输入描述:
- 第一行为数组numbers的长度
- 第二行为数组numbers的值每个数字通过空格分开
- 第三行输入为N,表示获取的次数
输出描述:按照题目要求能获取的最大数值
输入
7
1 2 2 7 3 6 1
3
输出
10
输入
3
1 2 3
3
输出
6
说明
全部获取所有的香蕉,因此最终根数为1+2+3 = 6function getMaxBanner (length, banners, count) {
let bannersArr = banners.split(' ');
let totalBanner = bannersArr.recuce((acc, cur) => {
return acc + cur;
}, 0);
if (count === bannersArr.length) {
return totalBanner;
}
let minWindowSum = Infinity;
let windowSize = length - count;
let currentWindowCount = 0;
for (let i = 0; i < windowSize; i++) {
currentWindowCount += bannersArr[i];
}
minWindowSum = currentWindowCount;
for (let i = windowSize; i < length; i++) {
currentWindowCount += (number[i] - number[i - windowSize]);
minWindowSum = Math.min(minWindowSum, currentWindowCount);
}
console.log(total - minWindowSum);
}