
算法7
灰度图存储
黑白图像常采用灰度图的方式存储,即图像的每个像素填充一个灰色阶段值,256节阶灰图是一个灰阶值取值范围为0-255的灰阶矩阵,0表示全黑,255表示全白,范围内的其他值表示不同的灰度。
但在计算机中实际存储时,会使用压缩算法,其中一个种压缩格式描述如如下:
10 10 255 34 0 1 255 8 0 3 255 6 0 5 255 4 0 7 255 2 0 9 255 21
所有的数值以空格分隔; 前两个数分别表示矩阵的行数和列数; 从第三个数开始,每两个数一组,每组第一个数是灰阶值,第二个数表示该灰阶值从左到右,从上到下(可理解为二维数组按行存储在一维矩阵中)的连续像素个数。比如题目所述的例子, “255 34” 表示有连续 34 个像素的灰阶值是 255。 如下图所:连续34个255,1个0 再来连续8个255。
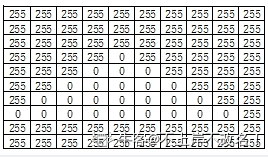
如此,图像软件在打开此格式灰度图的时候,就可以根据此算法从压缩数据恢复出原始灰度图矩阵。
请从输入的压缩数恢复灰度图原始矩阵,并返回指定像素的灰阶值。
输入描述:
输入包行两行,第一行是灰度图压缩数据,第二行表示一个像素位置的行号和列号,如 0 0 表示左上角像素。
备注:
1、系保证输入的压缩数据是合法有效的,不会出现数据起界、数值不合法等无法恢复的场景;
2、系统保证输入的像素坐标是合法的,不会出现不在矩阵中的像素;
3、矩阵的行和列数范图为:(0,100];
4、灰阶值取值范图:[0,255];
输出描述:输出数据表示的灰阶矩阵的指定像素的灰阶值。
10 10 255 34 0 1 255 8 0 3 255 6 0 5 255 4 0 7 255 2 0 9 255 21
3 4
99// line = '10 10 255 34 0 1 255 8 0 3 255 6 0 5 255 4 0 7 255 2 0 9 255 21'
// cords = '3 4'
function grayGraph (line, cords) {
let lineSplit = line.split(' ').map(Number);
let w = lineSplit[0];
let h = lineSplit[1];
let graph = lineSplit.slice(2);
const imageMatrix = [];
for (let i = 0; i < w; i++) {
imageMatrix[i] = new Array(h).fill(0);
}
let currentRow = 0;
let currentCol = 0;
let index = 0;
while (index < imageMatrix.length) {
let value = graph[index]
let count = graph[index + 1];
index += 2;
for (let i = 0; i < count; i++) {
imageMatrix[currentRow][currentCol++] = value;
if (currentCol === h) { // 换行
currentRow++;
currentCol = 0;
}
}
}
console.log(imageMatrix);
let [row, col] = cords.split(' ').map(Number);
console.log(imageMatrix[row][col]);
}手机APP防沉迷系统
智能手机方便了我们生活的同时,也侵占了我们不少的时间。“手机App防沉迷系统” 能够让我们每天合理的规划手机App使用时间,在正确的时间做正确的事
它的大概原理是这样的:
在一天24小时内,可注册每个App的允许使时段;
一个时间段只能使用一个APP, 不能在同时注册App2 和 App3;
App有优先级,数值越高,优先级越高。注册使用时段时,如果高优先级的App时间和低优先级的时段有冲突,则系统会自动注销低优先级的时段;
如果App的优先级相同,则后添加的App不能注册。
请编程实现,根据输入数据注册App,并根据输入的时间点,返回时间点注册的App名称,如果该时间点没有注册任何App,请返回字符串“NA"。
输入描述:
- 第一行表示注册的App数N
(N≤100) - 第二部分包括N 行,每行表示一条App注册数据
- 最后一行输入一个时间点,程序即返回注册点可App
2
App1 1 09:00 10:00
App2 2 11:00 11:30
09:30
数据说明如下
1、N行注册数据以空格分隔,四项数依次表示: App名称、优先级、起始时间,结束时间
2.优先级1-5,数字值越大,优先级越高
3、时间格式HH:MM,小时和分钟都是两位,不足两位前面补0
4.起始时间需小于结束时间,否则注册不上
5.注册信息中的时间段包含起始时间点,不包含结束时间点输出描述:输出一个字符串,表示App名称,或NA表示空闲时间。
输入:
1
App1 1 09:00 10:00
09:30
输出:
App1
说明:
App1注册在9点到10点间,9点半可用的应用名是App1
输入:
2
App1 1 09:00 10:00
App2 2 09:10 09:30
09:20
输出:
App2
说明:
ApP1和App2的时段有冲突,App2优先级高,注册App2之后,App1自动注销,因此输出App2题解
这是一个模拟题,需要按照题目描述的规则模拟注册过程,并在给定时间点找到注册的App。
程序的解题思路和关键步骤:
定义一个App类,用于表示应用程序对象,包括应用程序名称、优先级、开始时间和结束时间。同时,在App类中实现一个方法判断两个应用程序对象是否有时间重叠。
编写convertToMinutes方法,将时间字符串转换为分钟表示的整数。
编写convertToApp方法,将输入的字符串转换为应用程序对象。
通过读取输入,获取应用程序的数量,以及每个应用程序的注册信息。将注册信息转换为App对象,并根据题目规则进行注册。如果新注册的应用程序与已有的应用程序有时间重叠,根据优先级判断是否需要注销低优先级的应用程序。
读取给定的时间点,将其转换为分钟表示的整数。
遍历已注册的应用程序列表,找到包含给定时间的应用程序。
输出结果。
该程序使用了类的封装和集合的操作,通过遍历和比较,实现了应用程序的注册和冲突处理。最后,根据给定时间点找到相应的应用程序并输出结果。
时间复杂度:O(N^2),其中N为应用程序的数量。在每次注册应用程序时,都需要遍历已有的应用程序列表,判断是否有时间重叠。
空间复杂度:O(N),存储了已注册的应用程序列表// appNums = 2
// appUseDataStr = ['App1 1 09:00 10:00', 'App2 2 11:00 11:30']
// time = '09:30'
function convertTime (timeStr) {
const [hours, minutes] = timeStr.split(':').map(Number);
return hours * 60 + minutes;
}
function appUseTime (appNums, appUseDataStr, time) {
const apps = appUseDataStr.map(value => {
let split = value.split(' ');
return {
name: split[0],
priority: parseInt(split[1]),
startTime: convertTime(split[2]),
endTime: convertTime(split[3]),
}
})
let queryTime = convertTime(time);
const registerApps = [];
for (let i = 0; i < apps.length; i++) {
let app = apps[i];
if (app.startTime > app.endTime) {
continue;
}
for (let j = registerApps.length - 1; j >= 0; j--) {
let registerApp = registerApps[j];
if (Math.max(app.startTime, registerApp.startTime) < Math.min(app.endTime, registerApp.endTime)) {
if (app.priority > registerApp.priority) {
// 注销优先级低的应用
registerApps.splice(j, 1);
} else {
// 优先级不高,继续检查下一个已注册app
continue;
}
}
}
registerApps.push(app);
}
let result = 'NA'
for (let app of registerApps) {
if (queryTime >= app.startTime && queryTime < app.endTime) {
result = app.name;
break;
}
}
console.log(result);
}小朋友来自多少小区
幼儿园组织活动,老师布置了一个任务:
每个小朋友去了解与自己同一个小区的小朋友还有几个。
我们将这些数量汇总到数组 garden 中。
请根据这些小朋友给出的信息,计算班级小朋友至少来自几个小区?
输入描述:
输入:garden[] = 3
- garden 数组长度最大为 999
- 每个小区的小朋友数量最多 1000 人,也就是 garden[i] 的范围为 [0, 999]
输出描述:
输出:7
const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
})
rl.on('line', (line) => {
const input = line.split(' ');
const zones = new Array(1000).fill(0);
let result = 0;
let index = 0;
while (true) {
if (index >= input.length) {
break;
} else {
zones[input[index]] += 1;
}
index += 1;
}
for (let i = 0; i < 1000; i++) {
if (zones[i] <= 0) {
continue;
} else {
let total = Math.ceil(zones[i] / (i + 1));
result += total * (i + 1);
}
}
console.log(result);
rl.close();
})
function aaa ([2, 2, 3]) {
const zones = new Array(1000).fill(0);
let result = 0;
let index = 0;
while (true) {
if (index >= input.length) {
break;
} else {
zones[input[index]] += 1;
}
index += 1;
}
for (let i = 0; i < 1000; i++) {
if (zones[i] <= 0) {
continue;
} else {
let total = Math.ceil(zones[i] / (i + 1));
console.log(total, i + 1, total * (i + 1));
result += total * (i + 1);
}
}
console.log(result);
}测试用例执行计划
某个产品当前迭代周期内有N个特性(F1, F2, ..., FN)需要进行覆盖测试,每个特性都被评估了对应的优先级,特性使用其ID作为下标进行标识。
设计了M个测试用例(T1, T2,...,TM),每个用例对应了一个覆盖特性的集合,测试用例使用其ID作为下标进行标识,测试用例的优先级定义为其覆盖的特性的优先级之和。
在开展测试之前,需要制定测试用例的执行顺序,规则为:优先级大的用例先执行,如果存在优先级相同的用例,用例ID小的先执行。
输入描述:
- 第一行输入为N和M,N表示特性的数量,M表示测试用例的数量。
- 之后N行表示特性ID=1到特性ID=N的优先级。
- 再接下来M行表示测试用例ID=1到测试用例ID=M关联的特性的ID的列表。
输出描述:按照执行顺序(优先级从大到小)输出测试用例的ID,每行一个ID。
输入:5 4
1
1
2
3
5
1 2 3
1 4
3 4 5
2 3 4
输出:3 4 1 2
说明:测试用例的优先级计算如下:
T1=Pf1+Pf2+Pf3=1+1+2=4
T2=Pf1+Pf4=1+3=4
T3=Pf3+Pf4+Pf5=2+3+5=10
T4=Pf2+Pf3+Pf4=1+2+3=6
按照优先级从小到大,以及相同优先级,ID小的先执行的规则,执行顺序为T3,T4,T1,T2const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
})
let inputs = []
rl.on('line', (line) => {
inputs.push(line);
}).on('close', () => {
let [M, N] = inputs.shift().split(' ').map(Number);
let featuresNums = inputs.slice(0, N).map(Number);
let testCases = inputs.slice(N).map((line, index) => {
let sum = line.split(' ').reduce((acc, cur) => {
return acc + featuresNums[index];
})
return {
id: index + 1,
priority: sum,
}
})
testCases.sort((a, b) => {
return b.proiority - a.priority || a.id - b.id;
})
testCases.forEach(testCase => {
console.log(testCase.id)
})
})螺旋数字矩阵
疫情期间,小明隔离在家,百无聊赖,在纸上写数字玩。他发明了一种写法:
给出数字个数n和行数m (0 < n <= 999,0 < m <= 999),从左上角的1开始,按照顺时针螺旋向内写方式,依次写出2,3...n,最终形成一个m行矩阵。
小明对这个矩阵有些要求:
- 每行数字的个数一样多
- 列的数量尽可能少
- 填充数字时优先填充外部
- 数字不够时,使用单个*号占位
输入描述:两个整数,空格隔开,依次表示n、m
输出描述:符合要求的唯一矩阵
输入:
9 4
输出:
1 2 3
* * 4
9 * 5
8 7 6
说明:
9个数字写成4行,最少需要3列
输入:
3 5
输出
1
2
3
*
*
说明
3个数字写5行,只有一列,数字不够用*号填充这是一个模拟题,主要考察对矩阵的遍历和填充的能力。
首先,通过输入获取数字个数n和行数m。
计算矩阵的列数cols,根据题意,最少需要的列数是(n-1) / m + 1。
初始化一个大小为m行cols列的矩阵,所有元素初始值为"*"。
使用四个变量top、bottom、left、right来表示当前矩阵的上下左右边界。
使用cur变量表示当前要填充的数字,从1开始。
进入循环,按照顺时针螺旋的方式依次填充矩阵的数字。
从左到右:遍历当前行的左右范围,依次填充数字。
从上到下:遍历当前列的上下范围,依次填充数字。
从右到左:遍历当前行的右左范围,依次填充数字。
从下到上:遍历当前列的下上范围,依次填充数字。
在每次填充后,更新相应的边界。
循环直到所有数字都填充完毕。
最后,输出填充好的矩阵。
这样,通过模拟顺时针螺旋填充的过程,就能得到符合要求的矩阵。// m 行数
// n 数字个数
function getRoundArr (m, n) {
let cols = Math.ceil(n / m);
let matrix = Array.from({ length: m }, () => {
return Array(cols).fill('*')
})
let start = 1;
let top = 0;
let bottom = m - 1;
let left = 0;
let right = cols - 1;
while (start <= n) {
// 从左到右
for (let i = left; i <= right && start <= n; i++) {
matrix[top][i] = start++;
}
top++; // 上边界下移动
// 从上到下
for (let i = top; i <= bottom && start <= n; i++) {
matrix[i][right] = start++;
}
right--;
// 从右到左
for (let i = right; i >= left && start <= n; i--) {
matrix[bottom][i] = start++;
}
bottom--;
// 从下到上
for (let i = bottom; i >= top && start <= n; i--) {
matrix[i][left] = start++;
}
left++;
}
console.log(matrix);
}堆内存申请
有一个总空间为100字节的堆,现要从中新申请一块内存,内存分配原则为:
优先分配紧接着前一块已使用的内存,分配空间足够时分配最接近申请大小的空闲内存。
输入描述:
- 第1行是1个整数,表示期望申请的内存字节数。
- 第2到第N行是用空格分割的两个整数,表示当前已分配的内存的情况,每一行表示一块已分配的连续内存空间,每行的第1个和第2个整数分别表示偏移地址和内存块大小,如: 0 1 3 2 表示0偏移地址开始的1个字节和3偏移地址开始的2个字节已被分配,其余内存空闲。
输出描述:
- 若申请成功,输出申请到内存的偏移 若申请失败,输出-1。
备注:
- 若输入信息不合法或无效,则申请失败
- 若没有足够的空间供分配,则申请失败
- 堆内存信息有区域重叠或有非法值等都是无效输入
输入:
1
0 1
3 2
输出:
1
说明:
堆中已使用的两块内存是偏移从0开始的1字节和偏移从3开始的2字节,空闲的两块内存是偏移从1开始2个字节和偏移从5开始95字节根据分配原则,新申请的内存应从1开始分配1个字节,所以输出偏移为1。const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
})
let mallocSize; // 需要分配的内存大小
let useMemory = []; // 已分配的内存
rl.on('line', (line) => {
if (!mallocSize) {
mallocSize = parseInt(line.trim());
if (mallocSize <= 0 || mallocSize > 100) {
console.log(-1)
process.exit(0);
}
} else {
const memoryBlock = line.split(' ').map(Number);
useMemory.push(memoryBlock);
}
}).on('close', () => {
useMemory.sort((a, b) => a[0] - b[0]);
let start = 0;
let bestFitStart = -1;
let minSizeDiff = Number.MAX_SAFE_INTEGER;
for (let block of useMemory) {
let blockStart = block[0];
let blockSize = block[1];
if (blockStart < start || blockStart <= 0 || blockStart + blockSize > 100) {
console.log(-1)
process.exit(0);
}
let freeSpace = blockStart - start
// 空闲空间
if (mallocSize <= freeSpace && (freeSpece - mallocSize) < minSizeDiff) {
bestFitStart = blockStart;
minSizeDiff = freeSpace - mallocSize;
}
start = blockStart + blockSize;
}
// 检查最后一个内存块是否有足够空间
if (100 - start >= mallocSize && (100 -start-mallocsize) < minSizeDiff) {
bestFitStart = start;
}
console.log(bestFitStart)
})单行道汽车通行时间
M(1<=M<=20)辆车需要在一条不能超车的单行道到达终点,起点到终点的距离为N(1<=N<=400)。速度快的车追上前车后,只能以前车的速度继续行驶。求最后一车辆到达目的地花费的时间。
注:每辆车固定间隔一小时出发,比如第一辆车0时出发,第二辆车1时出发,以此类推
输入描述:
- 第一行两个数字:M N分别代表车辆数和到终点的距离,以空格分隔。
- 接下来M行,每行1个数字S,代表每辆车的速度。
0<S<30。
输出描述:
最后一辆车到达目的地花费的时间
2 11
3
2
输出 5.5const readline = require('readline');
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
})
let inputs = []
rl.on('line', (line) => {
lines.push(line)
}).on('close', () => {
const [M, N] = lines[0].split(' ').map(Number)
const speeds = lines.slice(1, M + 1).map(Number)
const arrivalTimes = new Array(M).fill(0)
arrivalTimes[0] = N / speeds[0]
for (let index = 1; index < M; index++) {
const currentTime = N / speeds[index] + index;
if (currentTime > arrivalTimes[index - 1]) {
arrivalTimes[index] = currentTime;
} else {
arrivalTimes[index] = arrivalTimes[index - 1];
}
}
console.log(arrivalTimes[M - 1] - M + 1)
})